【LeetCode刷题笔记】

常用数据结构

前缀树

在计算机科学中，trie，又称前缀树或字典树，是一种有序树，用于保存关联数组，其中的键通常是字符串。与二叉查找树不同，键不是直接保存在节点中，而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀，也就是这个节点对应的字符串，而根节点对应空字符串。一般情况下，不是所有的节点都有对应的值，只有叶子节点和部分内部节点所对应的键才有相关的值。

简单实现：

// 前缀树结构
type Trie struct {
    children map[rune]*Trie
    isEnd    bool
}

func NewTrie() *Trie {
    return &Trie{children: make(map[rune]*Trie)}
}

// 插入字符串
func (t *Trie) Insert(word string) {
    current := t
    for _, r := range word {
        if current.children[r] == nil {
            current.children[r] = &Trie{children: make(map[rune]*Trie)}
        }
        current = current.children[r]
    }
    current.isEnd = true
}

// 搜索字符串
func (t *Trie) Search(word string) bool {
    current := t
    for _, r := range word {
        if current.children[r] == nil {
            return false
        }
        current = current.children[r]
    }
    return current.isEnd
}

LeetCode范例：

• 剑指 Offer II 063. 替换单词
• 剑指 Offer II 065. 最短的单词编码

注意事项：
标记 isEnd 位于当前节点的下一节点，即 a->b->c->isEnd

并查集

常见题型

数组

数组子集问题

剑指 Offer II 079. 所有子集 - 力扣（Leetcode）
思路：
令 n = nums.length，由于 n <= 10，数组长度不长，所以可以考虑用一串长度为 n 的二进制串来表示各位要不要取（0：不取，1：取），那么共有 $2^n$ 种状态，以 nums = [1, 2, 3] 为例：

二进制串	子数组	二进制串对应十进制数
000	[]	0
001	[3]	1
010	[2]	2
011	[2,3]	3
100	[1]	4
101	[1,3]	5
110	[1,2]	6
111	[1,2,3]	7
那么遍历每种状态即可
代码实现如下：

func subsets(nums []int) [][]int {
    ans := [][]int{}
    n := len(nums)
    // 遍历每种状态 [0, 2^n)
    for i := 0; i < (1 << n); i++ {
        subArr := []int{}
        // 遍历nums数组，将二进制串中的 1 对应的数加入结果中
        for j := 0; j < n; j++ {
            if i & (1 << j) > 0 {
                subArr = append(subArr, nums[j])
            }
        }
        ans = append(ans, subArr)
    }
    return ans
}

数组全排列

46. 全排列 - 力扣（LeetCode）
这类问题需要用到回溯算法，在解决之前最好先自己画一下回溯树来捋清楚关系！

图片来自46. 全排列 题解 - 力扣（LeetCode）

回溯模板：

func backtrack() {
	if 满足终止条件 {
		将当前结果添加到最终结果中
		return
	}
	
    for (选择：本层集合中元素(树中节点孩子的数量就是集合的大小)) {
        处理节点
        backtrack()
        回溯，撤销处理结果
    }
}

代码实现：

func permute(nums []int) [][]int {

	// 初始化变量
    res := [][]int{}  
    n := len(nums)  
    path := make([]int, 0)  
    visited := make([]bool, n)

	// 定义递归函数
    var backtrack func()  
    backtrack = func() {
	    // 触发终止条件
        if len(path) == n {  
            tmp := make([]int, n)  
            copy(tmp, path)   
			res = append(res, tmp)  
            return  
        }
        // 遍历元素  
        for i, num := range nums {  
            if visited[i] {  
                continue  
            }  
            path = append(path, num)  
            visited[i] = true  
            backtrack()  
            path = path[:len(path)-1]  
            visited[i] = false  
        }  
    }  
    backtrack()  
    return res  
}

数组中第 K 个最大元素

215. 数组中的第K个最大元素 - 力扣（LeetCode）
视频讲解：7-2「力扣」第 215 题：数组中的第 K个最大元素_哔哩哔哩_bilibili
求解一个数组中的第 $k$ 大元素，最朴素的想法是对数组进行排序，如何取数组中的第 $n-k$ 个元素即为第 $k$ 大元素。但是这样解决，就算使用高效的快速排序，时间复杂度也只能是 $O(nlogn)$，无法达到题目要求的 $O(n)$，故可以在快排的基础上进行改进（快速选择），来达到 $O(n)$ 的复杂度。

我们知道快排中的 patition 是用来选出一个枢轴元素（pivot），将数组中的元素划分为大于 nums[pivot] 及小于 nums[pivot]两部分，如果此时的 pivot 正好等于 $n-k$ ，则说明此时的 pivot 处的元素就是第 $k$ 大元素。循着这个逻辑就可以利用二分思想缩小范围，直到 pivot 正好等于 $n-k$。

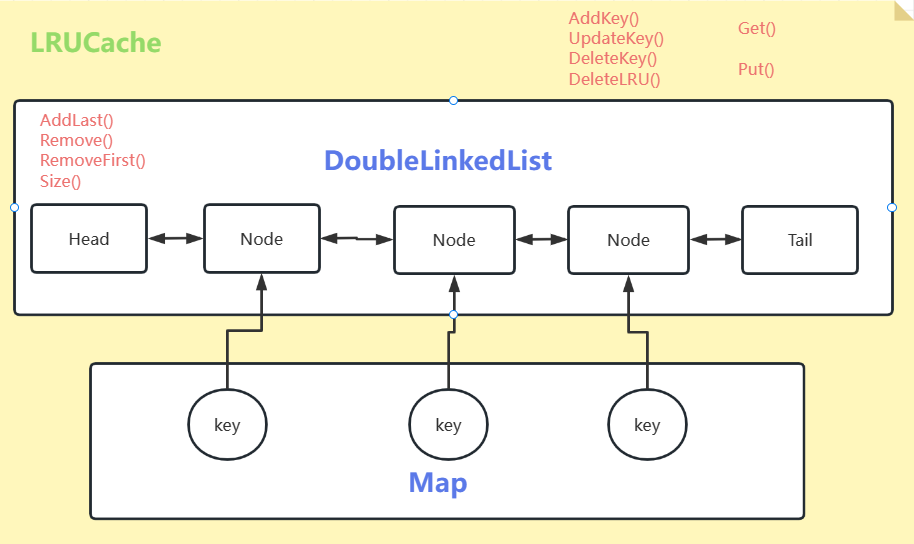
链表

LRU 缓存

146. LRU 缓存 - 力扣（LeetCode）

实现 LRUCache 主要需要用到哈希链表，所以本题也可以转换为实现一个 LinkedHashMap
哈希链表由一个 Map 和一个 双向链表 组成，双向链表是有序的，Map 可以帮助快速访问到链表中的结点。双向链表中包含了 Cache 中所需的 key、val 字段，Map 对 key 及对应的结点进行了映射 （key -> *Node）

具体代码实现如下：

type Node struct {  
   key   int  
   value int  
   next *Node  
   pre *Node  
}  
  
// 实现双向链表  
type DoubleLinkedList struct {  
   head *Node  
   tail *Node  
   size int  
}  
  
func InitList() DoubleLinkedList {  
   head, tail := &Node{key:0,value:0}, &Node{key:0,value:0}  
   head.next = tail  
   tail.pre = head  
   return DoubleLinkedList{  
      head: head,  
      tail: tail,  
      size: 0,  
   }  
}  
  
func (dll *DoubleLinkedList) AddLast(node *Node) {  
   pre := dll.tail.pre  
   pre.next = node  
   node.pre = pre  
   node.next = dll.tail  
   dll.tail.pre = node  
   dll.size++  
}  
  
func (dll *DoubleLinkedList) Remove(node *Node) {  
   node.pre.next = node.next  
   node.next.pre = node.pre  
   dll.size--  
}  
  
func (dll *DoubleLinkedList) RemoveFirst() *Node {  
   if dll.head.next == dll.tail {  
      return nil  
   }  
   first := dll.head.next  
   dll.Remove(first)  
   return first  
}  
  
func (dll *DoubleLinkedList) Size() int {  
   return dll.size  
}  
  
type LRUCache struct {  
   // {key : *Node}  
   mp map[int]*Node  
   cache DoubleLinkedList  
   capacity int  
}  
  
func Constructor(capacity int) LRUCache {  
   return LRUCache{  
      mp: make(map[int]*Node),  
      cache: InitList(),  
      capacity: capacity,  
   }  
}  
  
  
// 插入的key在缓存中已有时，更新key  
func (this *LRUCache) UpdateKey(key int) {  
   // 获取key对应的结点  
   node := this.mp[key]  
   // 从链表中移除对应结点  
   this.cache.Remove(node)  
   // 在链表尾部插入对应结点  
   this.cache.AddLast(node)  
}  

// 下面三个方法是对 LRUCache 中 map 和 cache 方法的进一步封装

// 添加某个key  
func (this *LRUCache) AddKey(key, val int) {  
   node := &Node{  
      key: key,  
      value: val,  
   }  
   this.cache.AddLast(node)  
   this.mp[key] = node  
}  
  
// 删除某个key  
func (this *LRUCache) DeleteKey(key int) {  
   node := this.mp[key]  
   this.cache.Remove(node)  
   delete(this.mp, key)  
}  
  
// 删除最近最久未使用key  
func (this *LRUCache) DeleteLRU() {  
   LRUNode := this.cache.RemoveFirst()  
   delete(this.mp, LRUNode.key)  
}  
  

func (this *LRUCache) Get(key int) int {  
   if this.mp[key] == nil {  
      return -1  
   }  
   this.UpdateKey(key)  
   return this.mp[key].value  
}  
  
  
func (this *LRUCache) Put(key int, value int)  {  
   if this.mp[key] != nil {  
      this.DeleteKey(key)  
      this.AddKey(key, value)  
      return  
   }  
   if this.cache.Size() >= this.capacity {  
      this.DeleteLRU()  
   }  
   this.AddKey(key, value)  
}

动态规划

最长递增子序列

300. 最长递增子序列 - 力扣（LeetCode）
这种子序列问题一般联想到动态规划方法或者贪心算法，本题使用动态规划算法
动态规划步骤：

1. 定义状态
   令 $dp[i]$ 表示以 $nums[i]$ 结尾的【最长上升子序列】的长度（这个定义中 $nums[i]$ 必须是被选取的）
2. 转台转移方程
   $dp[i]= \max_{0≤j<i,nums[j]<nums[i]} ​dp[j]+1$
3. 初始化
   $dp[i]=1$
4. 输出
   最后一个状态只表示以 $nums[len(nums)-1]$ 结尾的【最长上升子序列】的长度，应该返回的是 $dp[i]$ 中的最大值
5. 空间优化
   遍历到一个新数的时候，之前所有的状态值都得保留，因此无法优化空间。

   func lengthOfLIS(nums []int) int {
       n := len(nums)
       if n == 1 {
           return n
       }
       res := 0
       dp := make([]int, n)
       for i := range dp {
           dp[i] = 1
       }
       for i := 1; i < n; i++ {
           for j := 0; j < i; j++ {
               if nums[j] < nums[i] {
                   dp[i] = max(dp[i], dp[j] + 1)
               }
           }
       }
       for _, num := range dp {
           res = max(res, num)
       }
       return res
   }

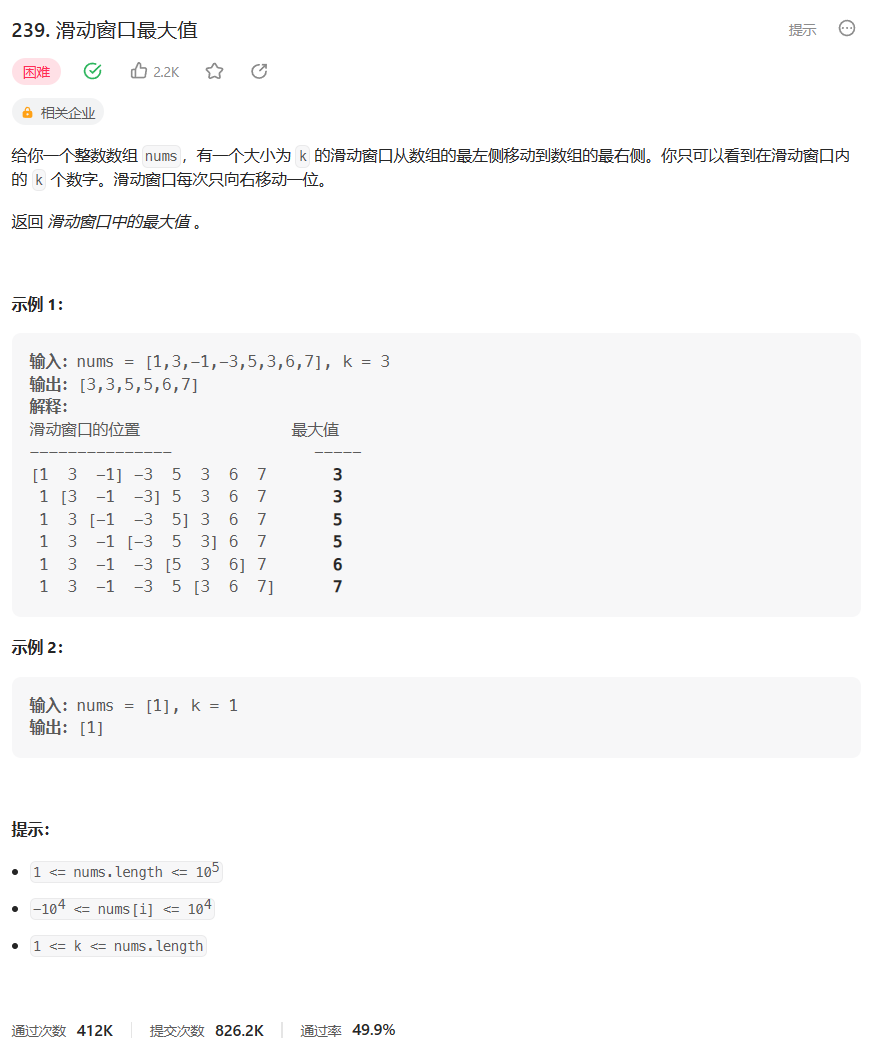
滑动窗口

滑动窗口的最大值

239. 滑动窗口最大值 - 力扣（LeetCode）

两种思路：

1. 使用优先队列（堆）存储滑动窗口中最大值的下标，然后滑动窗口每次移动，调整堆中的元素
2. 使用单调栈！维护一个单调递减的栈。

   type dq struct {  
      queue []int  
   }  
     
   func InitDQ() *dq {  
      return &dq{  
         queue: make([]int, 0),  
      }  
   }  
     
   func (q *dq) Front() int {  
      return q.queue[0]  
   }  
     
   func (q *dq) Rear() int {  
      return q.queue[len(q.queue)-1]  
   }  
     
   func (q *dq) Empty() bool {  
      return len(q.queue) == 0  
   }  
     
   func (q *dq) Push(val int) {  
      for !q.Empty() && val > q.Rear() {  
         q.queue = q.queue[:len(q.queue)-1]  
      }  
      q.queue = append(q.queue, val)  
   }  
     
   func (q *dq) Pop(val int) {  
      if !q.Empty() && val == q.Front() {  
         q.queue = q.queue[1:]  
      }  
      return  
   }  
     
   func maxSlidingWindow(nums []int, k int) []int {  
      queue := InitDQ()  
      n := len(nums)  
      res := make([]int, 0)  
      for i := 0; i < k; i++ {  
         queue.Push(nums[i])  
      }  
      res = append(res, queue.Front())  
      for i := k; i < n; i++ {  
         queue.Pop(nums[i-k])  
         queue.Push(nums[i])  
         res = append(res, queue.Front())  
      }  
      return res  
   }