本文梳理基于 Isolation Forest（IF）的若干拓展算法

关于 IF 的相关知识我在之前的文章【机器学习】异常检测文献阅读：关键算法篇 中进行了梳理

1 Extended Isolation Forest（EIF）

1.1 简介

原有的算法 IF 利用了异常数据总是少而与众不同的特点，通过一次次的随机分割数据建立隔离森林来分离出异常值，足够直观且高效。

然而分割数据的方式是每次分割是个数据的某一单一维度上进行的，所以每次运行的结果总会出现一定的偏差。

image-20210419210248189

通过 正态数据分布的异常分数图 可以看出，异常分数总是随着到某一数据中心的距离的增加而增加，IF单纯的从某一维度对数据切割，总会存在偏差。

image-20210419210219580

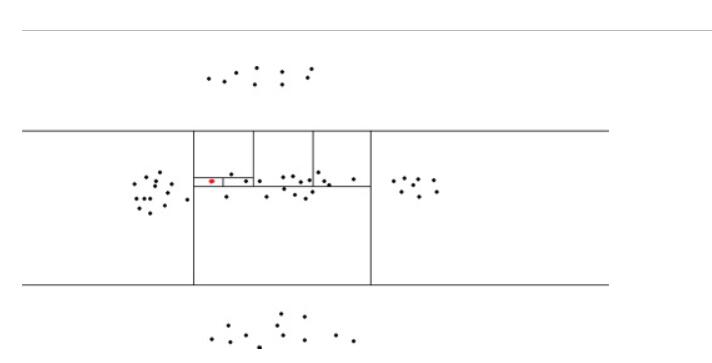
同样对于两簇正态分布的数据，使用 IF 不断选取单一维度进行切割，不难发现在数据右上角与左下角也会产生异常分数较低的簇（gohst clusters）（实际上这些位置的点应该为异常点）。

image-20210419210425081

对于正弦波形也是同理。

image-20210419210159784

试想我们如果可以斜着切割数据，那么就可以有效弥补这一不足。

在 EIF 中，对 IF 中的数据分割方式进行了改进，来弥补原有算法的缺陷。

改进的方法中，EIF 使用了一个拥有随机斜度（slopes）的超平面来对数据进行切割，该超平面不与坐标轴平行。

image-20210419210548911

1.2 算法描述

Isolation Forest 分支切口（branchs cuts）的信息：

  1. 一个随机选取的特征或坐标
  2. 一个来自于该特征的随机值

Extended Isolation Forest 分支切口信息：

  1. 一个分支切口的随机斜度（slope）
  2. 一个在数据集可用值范围内随机选择的截距（intercept）

image-20210429204912315

二维空间如此，高维空间（N 维）也是同理，只不过分支切口变味了一个 N -1 维的超平面

这些超平面同样被一个随机正交向量和一个随机截距点所确定，如二维情况类似

1.3 算法实现

image-20210420205349794 image-20210420205412696 image-20210420205437388

1.4 测试

image-20210419214517225 image-20210419214532878 image-20210420205557800 image-20210420205633002 image-20210420205650795

2 Fuzzy Set-Based Isolation Forest（FSBIS）

2.1 简介

文章在原有算法 IF 的基础上，提出通过对记录的属性的隶属度（membership）进行划分从而构建森林。

其中，隶属度是根据到样本中心（middle of the cluster）的距离（也就是属性的平均值）来确定的。

优点：

  • 直观
  • 返回异常值的隶属度几乎为零
  • 以返回异常程度的方式构造的函数不需要使用复杂的标准化公式
  • 运行时间并不比经典 IF 多，在某些情况下甚至短于经典 IF

2.2 算法描述

对于经典 IF 相对复杂的建树过程，FSBIS 提出了如下改进

  1. 在经典 IF 的第一阶段中，我们会从过滤后的簇（cluster）中所选择的属性的所有值中确定平均值 m，这个值会被存在相应的节点上

    1
    TODO 平均值m的具体确定方法？

    we always determine the average value of m from all the values of the chosen attribute located in the filtered cluster.

  2. 通过公式计算出已经构建好的簇的隶属度

    image-20210429204937140

  3. 最终，异常分数是每个节点所有隶属度之和

2.3 算法实例

image-20210422202750238 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
如上图所示，我们要计算异常分数的点是 （x， y） = （0.7， 0.6）

第一次划分：x = 0.5，过滤后得到黄色区域

黄色区域中心点 center #1 在 x = 0.8 处

故隶属度：p1 = 1 - (0.8 - 0.7) / (0.8 - 0.5) = 2/3

第二次划分：y = 0.7，过滤后得到红色区域

红色区域中心点 center #2 在 y = 0.3处

故隶属度：p2 = 1 - (0.6 - 0.3) / (0.7 - 0.3) = 1/4

第三次划分：x = 0.75，过滤后得到绿色区域

划分至绿色区域后，只剩下目标点，其隶属度不需要计算，因为明显是 1

最后该点的异常分数 2/3 + 1/4 = 11/12

构建的二叉树如下所示：

​ image-20210422204718182

2.4 算法实现

image-20210422205159551 image-20210422205241318 image-20210422205159551 image-20210422205241318

3 Efficient Anomaly Detection by Isolation Using Nearest Neighbour Ensemble

Advantage:

  • Compared with some nearest neighbour-based method, the proposed method has linear time complexity and constant space complexity.
  • Compared with tree-based isolation method iForest, the proposed isolation method overcomes three weaknesses of iForest
    • Its inability to detect local anomalies
    • anomalies with a low number of relevant attributes
    • anomalies that are surrounded by normal instances

Two important challenging:

  • the requirement of low computational cost
  • the susceptibility to issues in high-dimensional datasets

How to operate:

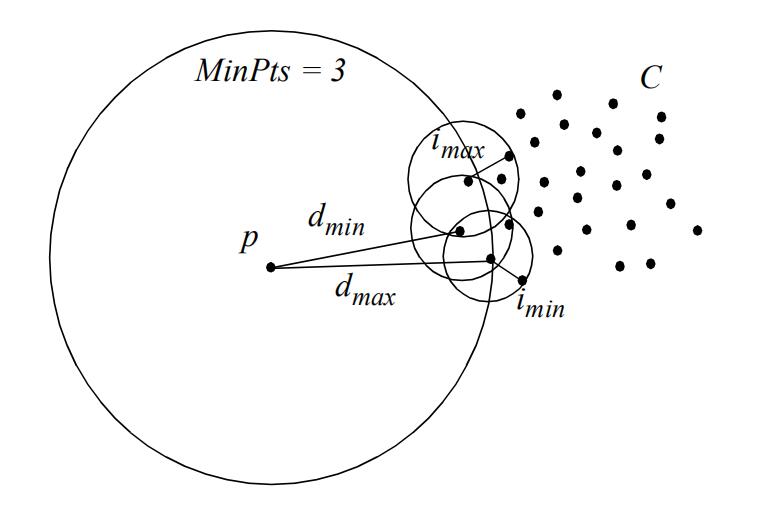
  • it partitions the data space into regions using a subsample and determines an isolation score for each region
  • each region is defined with a centre represented by an instance from the subsample; and its boundary is defined by the distance to the nearest neighbour of the instance at the centre.

The intuition behind iNNE:

  • an anomaly can be expected to be far from its nearest neighbour

Some definations:

  • Definition 1

    image-20210525210727558

  • Definition 2

    image-20210525210817030

  • Definition 3

image-20210525211202981 image-20210525211517695

  • Defination 4

    image-20210525211555777

    Where β is a user defined threshold.

  • Defination 5

    image-20210525211913605

  • Defination 6

    image-20210525212137950

  • Defination 7

    image-20210525212209132

  • Defination 8

    image-20210525212230930

$$\begin{pmatrix} 1/\sqrt{2} & 1/\sqrt{2} \ -1/\sqrt{2} & 1/\sqrt{2} \end{pmatrix} \begin{pmatrix} 1 & 2 & 3 \ 1 & 2 & 3 \end{pmatrix} = \begin{pmatrix} 2/\sqrt{2} & 4/\sqrt{2} & 6/\sqrt{2} \ 0 & 0 & 0 \end{pmatrix}$$

$$\begin{pmatrix} 1/\sqrt{2} & 1/\sqrt{2} \ -1/\sqrt{2} & 1/\sqrt{2} \end{pmatrix} \begin{pmatrix} 3 \ 2 \end{pmatrix} = \begin{pmatrix} 5/\sqrt{2} \ -1/\sqrt{2} \end{pmatrix}$$

$$\begin{pmatrix} p_1 \ p_2 \ \vdots \ p_R \end{pmatrix} \begin{pmatrix} a_1 & a_2 & \cdots & a_M \end{pmatrix} = \begin{pmatrix} p_1a_1 & p_1a_2 & \cdots & p_1a_M \ p_2a_1 & p_2a_2 & \cdots & p_2a_M \ \vdots & \vdots & \ddots & \vdots \ p_Ra_1 & p_Ra_2 & \cdots & p_Ra_M \end{pmatrix}$$

$$\begin{pmatrix} 1 & 1 & 2 & 4 & 2 \ 1 & 3 & 3 & 4 & 4 \end{pmatrix}$$

$$\begin{pmatrix} -1 & -1 & 0 & 2 & 0 \ -2 & 0 & 0 & 1 & 1 \end{pmatrix}$$

$$Var(a)=\frac{1}{m}\sum_{i=1}^m{(a_i-\mu)^2}$$

$$Cov(a,b)=\frac{1}{m}\sum_{i=1}^m{a_ib_i}$$

$$X=\begin{pmatrix} a_1 & a_2 & \cdots & a_m \ b_1 & b_2 & \cdots & b_m \end{pmatrix}$$

$$\frac{1}{m}XX^\mathsf{T}=\begin{pmatrix} \frac{1}{m}\sum_{i=1}^m{a_i^2} & \frac{1}{m}\sum_{i=1}^m{a_ib_i} \ \frac{1}{m}\sum_{i=1}^m{a_ib_i} & \frac{1}{m}\sum_{i=1}^m{b_i^2} \end{pmatrix}$$

$$\begin{array}{l l l} D & = & \frac{1}{m}YY^\mathsf{T} \ & = & \frac{1}{m}(PX)(PX)^\mathsf{T} \ & = & \frac{1}{m}PXX^\mathsf{T}P^\mathsf{T} \ & = & P(\frac{1}{m}XX^\mathsf{T})P^\mathsf{T} \ & = & PCP^\mathsf{T} \end{array}$$

$$E=\begin{pmatrix} e_1 & e_2 & \cdots & e_n \end{pmatrix}$$

$$E^\mathsf{T}CE=\Lambda=\begin{pmatrix} \lambda_1 & & & \ & \lambda_2 & & \ & & \ddots & \ & & & \lambda_n \end{pmatrix}$$

$$P=E^\mathsf{T}$$