【机器学习】异常检测文献阅读:基于K-Means的IForest
本文梳理论文 《K-Means-based isolation forest》
希望通过梳理这篇论文理清思路,以便获得启发
论文地址:https://www.sciencedirect.com/science/article/pii/S0950705120301064#tbl1
1 摘要
异常处理是数据科学领域中的重要问题,然而现有的异常检测模型还都有待提高:
- 不够高效
- 只能应用于单一领域
- 以非直觉(nonintuitive)的方式运行
在这篇论文中,我们对经典的 Isolation Forest 进行了分析,并且在它的基础上提出了基于 K-Means 的 IFoest
该方法的优点:
- 高效检测各种类型的异常值
- 使用户直观确定所分析数据集中单个样本的异常分数
- 能够在决策树构件的步骤中拟合数据
2 预备知识
2.1 K-Means
2.1.1 算法描述:
k-means 算法是无监督学习领域最为经典的算法之一。
在数据中选取多个点作为初始化的样本中心,所有样本选择距离自己最近的样本中心进行聚类,并在新生成的类中依据类中样本间的距离重新选择样本的样本中心,选择好新的样本中心后再根据所有样本到新样本中心的距离生成新的类,依此循环往复,直到达到某一限定条件(迭代次数、最小误差变化等)。

K-means 算法步骤为:
2.1.2 算法优化
由于生成类的数量 k 需要我们自己选定,所以需要一些选定 k 值的方法(手肘法、Gap statistic 方法)
本论文中使用手肘法选择 k 值:

本图中 Y 轴是样本距离之和,X 轴是 k 值,可以看出 k = 3 是拐点,故选择 3 作为 k 值
2.2 Isolation Forest
专家门在数据挖掘时通常会列出一些在异常检测领域比较高效的算法,Isolation Forest 几乎每次都会位列其中。
隔离森林通过随机选取属性与属性对应的值对所有数据进行切分,切分后得到两部分数据分别放入左右子树中,对左右子树继续进行上述操作,直到数据不能再分或树高达到上限高度,一棵 Isolation Tree 就构建成功了。
直观上,正常点通过多次切分也还是在同一层中,而异常点在切分的过程中更易被切分出去,所以异常点所在树的深度并不深,以此就能分离出异常点来。
我们可以依据某个点所在树的深度计算其异常分数值,树越浅,异常分数越高。
通过随机采样选取多组数据构建多棵 ITree,就能构建出一个完整的 Isolation Forest。
对某个点在各个树中的异常分数求平均,就能得到该点总的异常分数。

3 基于 K-Means 的 Isolation Forest
3.1 思想
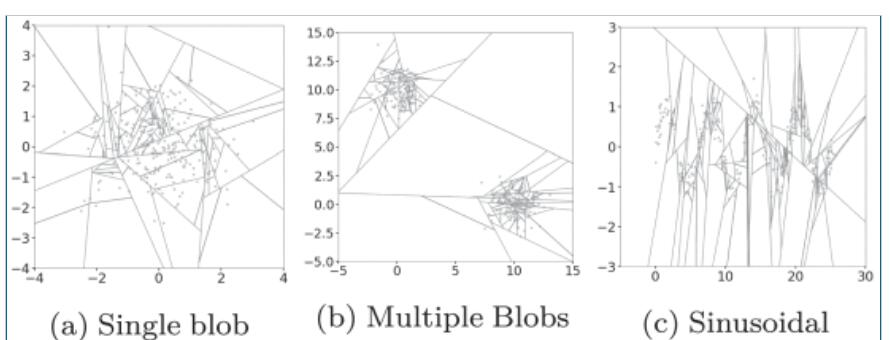
根据 IForest 中给出的图示我们可以看出,在对平面中的 x、y 交替划分了 10 次之后,我们分离出了红点。
可以注意到,无论这个点在是否接近分割区域的边界,最终的分割次数始终为 10(10 这个值最后被我们传入异常分数计算公式来计算异常分数)。这个方法是严格二分的,与分割点有关,因此异常分数与分割次数严管相关。
另外也可以注意到,该方法对直观上观察到的簇(clusters)不敏感。
因此我们可以对方法进行改进:对每次取得的属性对应的值进行 K-Means 聚类,得到的多个簇作为子节点重复之前的操作。
一棵树的叶子节点数取决于训练阶段数据集子分区中存在的最佳聚类数(也就是上文中通过手肘法决定的 k 值)。

3.2 具体算法
- 训练的初始阶段与经典的 IForest 相似,随机选取一个属性
q; - 使用 K-means 将属性
q中所有值划分为 k 个簇(k 值由手肘法选定); - 划分得到的 k 个簇作为根节点的叶子节点
- 对于每一个叶子节点,可以重复上述操作
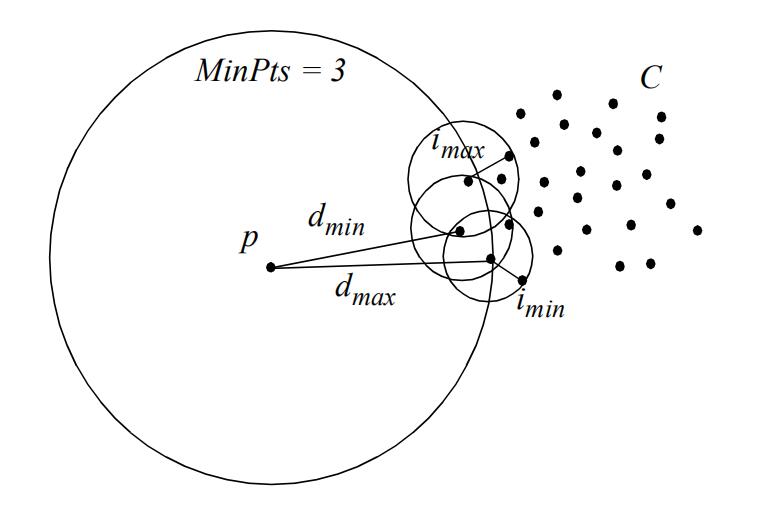
3.3 异常分数的计算
每次分割后得到的异常分数:

- c_q:簇的中心点
- c_l :簇的边界
- x :需要计算异常分数的点
- d(x, y):x 到 y 的距离
最终得分是每个数据在每次分割后得异常分数之和:

4 测试
选用 NYC taxi trip data 数据集进行测试


各数据集中 IForest 与 K-Means-based IF 执行时间效率对比: